It is one of the cheapest and the most prolific experimental systems I made. It is probably the simplest experimental system in which the period doubling route to chaos has been observed.

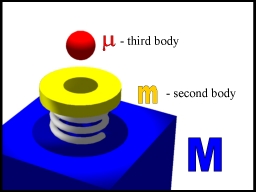
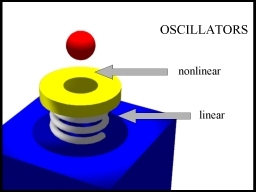
From the theoretical point of view the bouncing ball model - a system in which a ball bounces on a vibrating surface - can be seen either as a particular three body system or as a system of two coupled oscillators. One of the oscillators, (m, M) is linear. The other one, (m, M), is strongly non-linear.
 

1. a steel ball of diameter around 4 mm
2. a glass or plastic concave lens
3. a loudspeaker
4. an audio frequency generator

Observe (and listen to) the changing modes of the ball bouncing motion at the increasing amplitude of the surface vibrations.

Experiments that we performed allowed us to record a number of essential phenomena observed in the nonlinear systems.
To record the phenomena we were recording the phase of the consecutive collisions of the bouncing ball with the oscillating surface.
In the experiments the amplitude of the surface vibration was swept either up or down.
Here is list of the basic observations we made:

1. Their period-doubling routes to chaos.

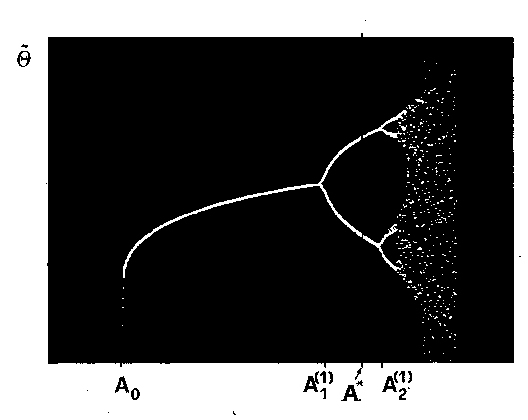
The picture below presents the bifurcation diagram of the BB system recorded in the experiment where the amplitude A of the surface vibrations was swept down. The bifircation diagram recorded in the experiment contains the simplest periodic mode and its period-doubled versions.




Here is the most interesting part of the diagram:



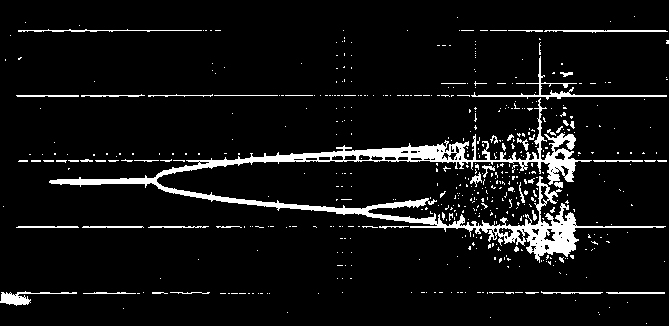
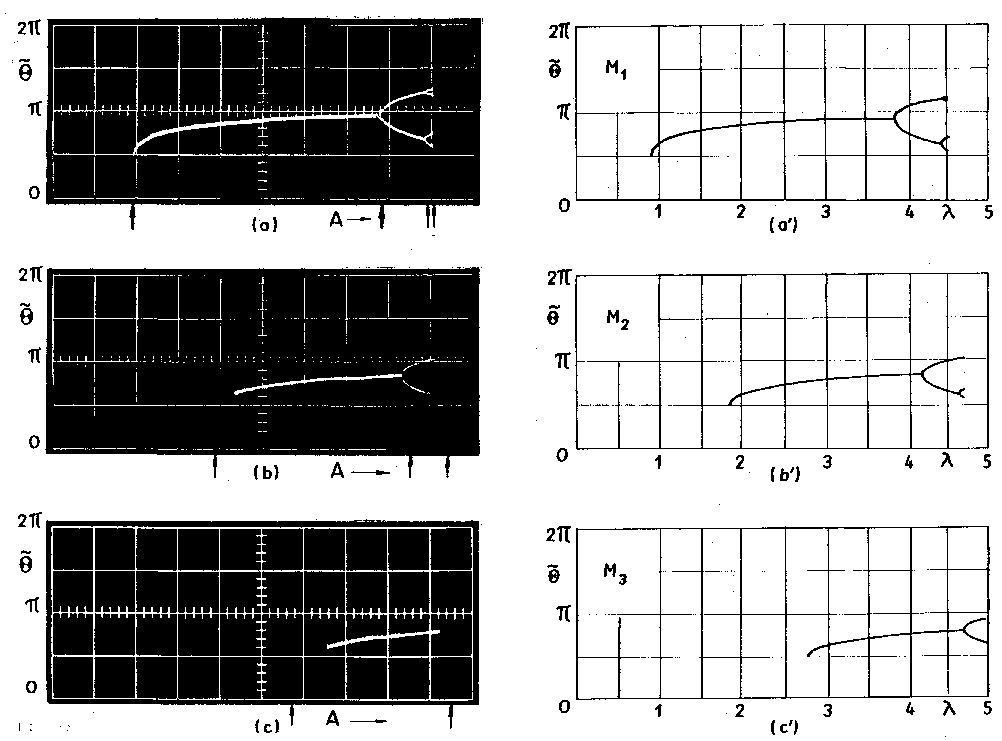
One of the most characteristic features of the nonlinear dynamical systems is that at the same value of the control parameter, here - the amplitude of the surface vibrations, the system may stay in a few coexisting vibration modes. The picture below (left) presents the bifurcation diagram of three of them denoted as M_1, M_2 and M_3. The diagrams presented on the right were obtained from numerical simulations of the laboratory experiments.



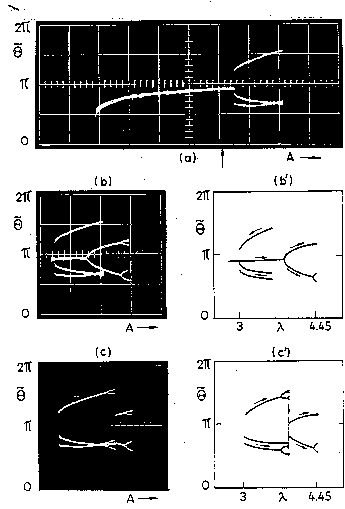
As we have found, apart from the simple periodic modes and their period-doubled variations it is possible to observe also their period-trippled versions. The picture below provides an experimental evidence.



All of the presented above modes of motion are described in detail in:

2. Critical slowing down and hysteresis around the bifurcation points.

The dynamics of the phase oscillations suffers a critical slowing down near the bifurcation points. Thus, moving up and down through the bifurcation diagrams at a finite rate causes inevitably hysteresis effects. The picture below presents the experimental evidence for the phenomenon and its numerical simulation:



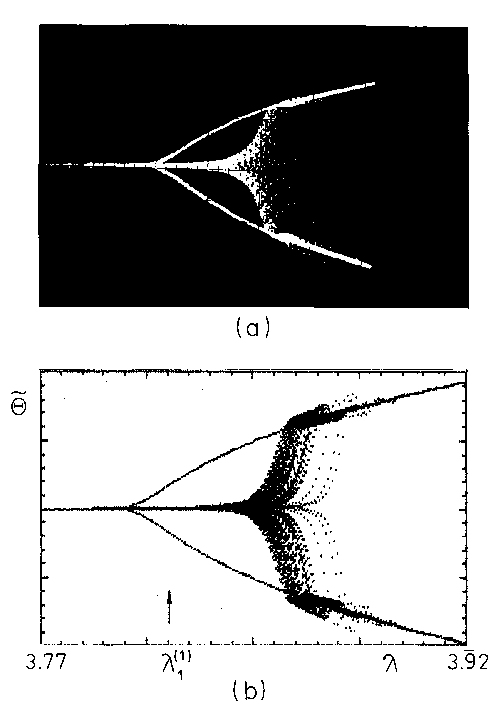
Notice the assymetry of the hysteresis effects. There is a large dispersion in sweeps up, while in sweeps down it is hardly visible. The phenomenon was explained in:

3. Resonances of the basic periodic modes.

Observing, at a given value A of the surface vibration amplitude, the phase of the consecutive collisions one finds that is behaves as a damped harmonic oscillator. Its resonant frequency depends on A. The frequency is thus different at different parts of the bifurcation diagram. The picture below presents the bifurcation diagrams recorded in presence of a periodic perturbation of  various fixed frequencies. Plots shown on the right were obtained from numerical simulations.

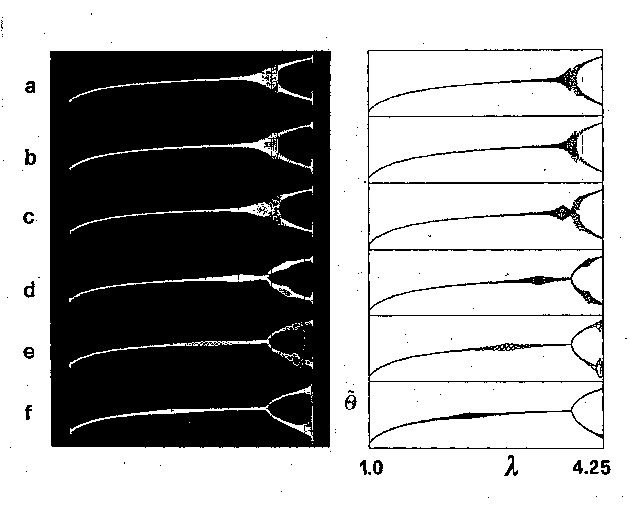
As seen in reordings (a), (b) and (c) above, where the frequency of the periodic perturbation was close to the half of the frequency of the surface vibration, the bifurcation was suppressed. Pictures below show this in more detail.

A virtual version of the experimental system is described in: Bouncing Ball Workbench.
Its DOS Pascal implementation is zipped together with a few other files needed to run it in: BBW

A high quality bouncing ball experimental set-up has been designed by Brad E. Paden.

A threepenny experiment on the ball bouncing on the motionless surface has been performed and carefully analysed by Éric Falcon & Stéphan Fauve.

P. Pieranski
Jumping particle model.  Period doubling cascade in an experimental system.
J. Phys. (Paris), 44, 573 (1983).

P. Pieranski, Z. Kowalik and M. Franaszek,
Jumping particle model.  A study of the phase space of a nonlinear dynamical system below its transition to chaos.
J. Phys. (Paris), 46, 681 (1985).

P. Pieranski and R. Bartolino,
Jumping particle model.  Modulation modes and resonant response to a periodic perturbation.
J. Phys. (Paris), 46, 687 (1985).

M. Franaszek and P.  Pieranski,
Jumping particle model.  Critical slowing down near the bifurcation points.
Can. J. Phys.  63, 488 (1985).

P. Pieranski and J. Malecki,
Noisy precursors and resonant properties of the period, doubling modes in a nonlinear dynamical system.
Phys. Rev.  A 34, 582 (1986).

P. Pieranski and J. Malecki,
Noise-sensitive hysteresis loops around period-doubling bifurcation points.
Nuovo Cim.  9, 757 (1987).

P. Pieranski,
Direct evidence for the suppression of period doubling ,  in the bouncing ball model.
Phys. Rev.  A 37, 1782 (1988).

Z. Kowalik, M. Franaszek and P.  Pieranski,
Self-reanimating chaos in the bouncing ball system.
Phys. Rev.  A 37, 4016 (1988).