SPAGHETTI KNOTS
Piotr Pieranski, Sandor Kasas, Giovanni
Dietler, Jacques Dubochet and Andrzej Stasiak, New Journal
of Physics
This is, I think, one of the most unusual and the
cheapest experiments ever made.
It was performed by Giovanni Dietler and Sandor
Kasas.
This is, what you need to repeat it:
1. a plate of well (not al dente)
cooked spaghetti.......0.50 $
2. a drop of olive oil...................................................0.01
$
--------------
Total.........0.51 $ (Salt not taken into account!)
Experiment 1.
Take one spaghetto.
Tie a knot on it and pull it by its ends. Gently!
Observe, where it breaks.
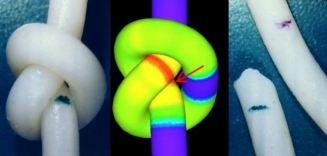
The peaks of curvature are seen as red rings
on the surface of the simulated knot.
To see a movie from the experiment jump to the Giovanni's
group pages:
http://www.unil.ch/ipmc/docs/gd/projects/knots/knots.html.
To see, how the peaks of curvature appear, when the knot is tightened, have
a look at this simulation.
Colors code the curvature: blue =>0, red >1.5.
Experiment 2.
Take one spaghetto.
Tie two different knots on it and pull it by its
ends. Gently!
Observe, which of the knot breaks first.
The problem we decided to study was serious. Let
me define it.
All people, whose life can be found hanging on
a piece of a rope, know well that the rope on which a knot is tied looses
a considerable fraction of its strength. Such a knotted rope breaks more easily
- invariably at the place at which the knot is tied. Why is it so? Where
exactly the breakage place is localized? These were the questions we wanted
to study.
To find out how the experiments were done and what
their conclusions are, have a look at the recently published New Journal
of Physics paper. You will find there also
an explanation why at all spaghetti was used - its choice might look funny,
but it was a necessity. The paper describes also a series of computer
experiments I made to find out the curvature profiles of knots tightened
by the SONO algorithm. The experiments
revealed a distinct peaks of curvature close to the entrance to the knots.
Spaghettis, and as we think also ropes, break at the peaks.
If you want to see how SONO ties virtual knots,
have a look at the animations: TyingTrefoil,
TyingFigureEight.
Knots tied by SONO are also tightened by it. Have a look at the tightenieng of the open trefoil knot (overhand
knot). Colors code the curvature: blue =>0, red >1.5.
The paper, obviously, attracts a lot of attention.
Below you will find a list of the www places at which it was discussed.
Doing anything new and unconventional one must take
into account the unexpected side effects of it. Had the spaghetti been excluded
as an experimental object (on the grounds that it is not a serious material),
we would have avoided possible problems. On the other hand, the explanation
why the ropes break on knots would have not been given. And, last but not
least, a lot of fun would have been lost as well ...
Pop-science paper
Piotr Pieranski, Zawieszeni na makaronie,
Wiedza i Zycie
Press reports
Mike Martin, Scientists use noodle to model DNA
mutation, UPI Science News
Piotr Cieslinski, Wezly na spaghetti, Gazeta
Wyborcza
Mark Henderson, Spaghetti solves a knotty problem,
The Times
Sanjida O'Connell, Spaghetti ties up knot theory,
The
Guardian
Robert Matthews, All in a knot, The
Daily Telegraph
Denis Delbecq, Etude de nœuds dans un plat de spaghettis
Liberation
Christian Herbst, Aufschlussreiche Spaghetti, Financial Times
http://unisci.com/stories/20012/0614013.htm
http://physics.about.com/library/news/bllatestnews.htm
http://www.scicom.hu.ic.ac.uk/students/news/spaghetti.htm
http://www.ananova.com/news_quirky/story/sm_326187.html
http://www.beyond2000.com/news/Jun_01/story_1186.html
