QUASI-QUANTIZATION OF WRITHE
In general, the tightening
of
a knot results in changes of its writhe. As the conformation of the
knot
tends to its most tight, hopefully ideal, conformation, its writhe
value
tends to a well defined limit. The picture below shows an example.
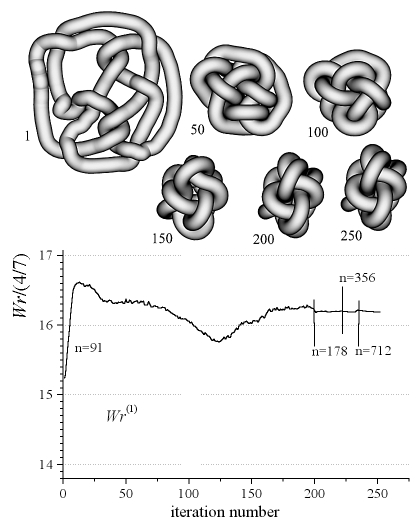
Fig. 1. Evolution of a loose conformation
of the
10.120 knot towards its most tight conformation. The evolution was
enforced
by SONO algorithm. Calculations started with a number of segments
N=91.
At the end of the tightening process the number of segments was doubled
3
times up to N=712.
Numerical experiments on all alternating
simple knots
with up to 10 crossings reveal, that the limit writhe values show a
visible
tendency to gather around equally spaced levels. As conjectured by
Stasiak
and Cerf, the spacing of the levels should be equal 4/7 [2]. Figure
below
confronts the theoretical prediction with results of the numerical
experiments.
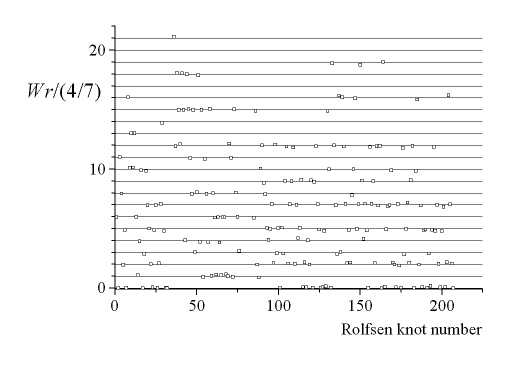
Fig. 2. Wr/(4/7) versus the knot
number for ideal conformations of all alternating prime knots with up
to 10 crossings. Horizontal lines indicate the writhe levels suggested
by Cerf and Stasiak. The gap visible in the set of plotted points in
the vicinity of the knot number=80
corresponds to the non-alternating knots with 9 crossings. A smaller
gap
localized around knot number=40 corresponds to 3 non-alternating knots
with
8 crossings.
Is the 4/7 spacing between the writhe levels
the optimal one? To answer the question we checked all values from 0 to
1. Figure
below shows the results of this check.
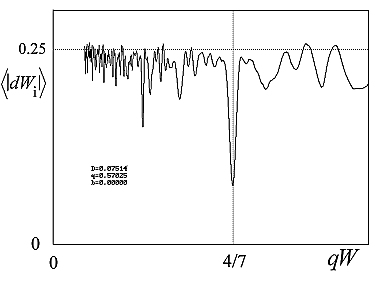
Fig. 3. The average relative deviation
<|dW|> of the writhe values of all alternating knots with up to
10 crossings from n*qW writhe levels versus the writhe quantum qW.
As seen in the figure above, the 4/7 quantum
fits best the numerical data. However, it as also clearly seen from the
figure, the fit is not perfect: the writhe values deviate from the
Stasiak-Cerf 4n/7 levels. The quantitative analysis of the
deviations is presented in the
figure below.
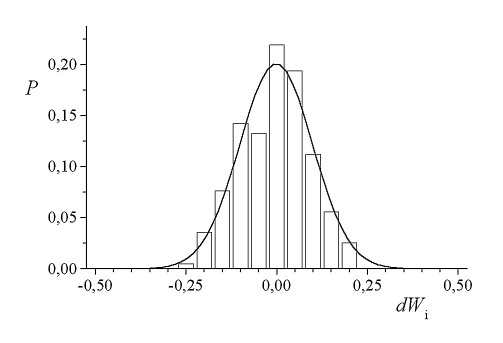
Fig. 4. The probability P of finding
a
the dW deviations within 20 counting bins. The Gaussian function which
fits
the data is also plotted; its half width equals 0.2.
The half width of the distribution of the
writhe deviations from the closest Cerf-Stasiak levels was shown to be
equal 0.2. In view of the analysis of numerical errors we performed,
deviations of such
a magnitude cannot be attributed to the inaccuracy of the writhe
calculations; they must be seen as the intrinsic property of the most
tight conformations found by the SONO algorithm. Will a different
algorithm of the determination of the ideal conformations substantially
reduce the value? Will it reduce it to zero? Is the writhe
quasi-quantization an approximate or an exact rule?
The questions posed above remain open.
Which is the possible practical implication of
the
writhe quasi-quantisation phenomenon? To get an insight into the
problem, imagine that you are trying to tie different knots, in their
most tight forms,
on a rope with an internal, parallel threads bundle structure. If at
the
end of the tying procedure splicing the ends of the rope one wants, for
some
reasons, to keep identity of the threads, the angle of the relative
orientation
of the meeting ends should be equal to a multiple of 2p. This happens when the writhe value of the knot
is
integer. From such a point of view, the tight conformations of the
knots
whose writhe values are grouped around a non integer writhe level are
more
difficult to tie than the tight conformations of knots whose writhe
value
stays close to an integer level. Have a look at the picture below in
which
two knots with a non integer and an integer values of writhe are
presented.

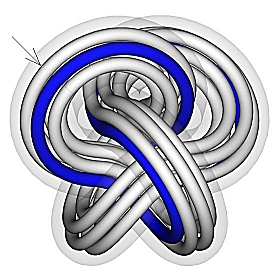
Fig. 5. The ideal 3.1 (left) and 4.1
(right) knots
tied on a rope with an internal structure. The parallel transport of
the
internal structure of the rope leads in the case of the 3.1 knot to a
distinct
misfit of the orientation of the meeting ends. The ends fit perfectly
well
in the case of the 4.1 knot – the arrow indicates the hardly visible
meeting
point.
[1] P. Pieranski, in Ideal Knots,
eds.
A. Stasiak, V. Katritch and L. H. Kauffmanm, World Scientific,
Singapore, 1998.
[2] C. Cerf and A. Stasiak, PNAS 97, 3795 (2000)
[3] P. Pieranski and S. Przybyl, Eur.Phys. J. E 6, 117
(2001).
[4] P. Hoidn, R. Kusner and A. Stasiak,
New J. Phys. 4, 20 (2002).
A pop-science article by Keith Devlin describing
the
writhe quantization phenomenon can be found in New Scientist.




