THE PROBLEM 
OF 
THE IDEAL TWISTED PAIR


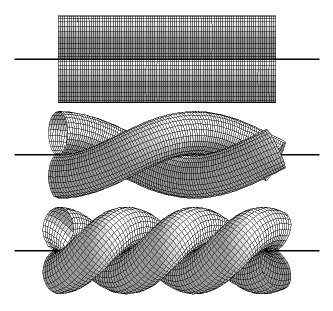
    Take two straight pieces of a perfect (perfectly flexible, but at the same time perfectly hard) rope and put them side by side. Now, start twisting the pair aiming at producing a periodic structure, which uses as little of the rope as possible per period i.e. per 2 crossings.
    The problem has been described in [1]. Below we present essential results.
 

TWISTED PAIR - TYPE 1

The simplest way of twisting two perfect ropes together is as follows:
(a) take two straight pieces of the rope and put them side by side so that they touch along a common line
(b) start twisting them together so that they remain in touch along the initial contact line,
(c) stop twisting, when the pitch of the structure equals Pi - overlaps are just about to appear.

The pitch of the tight periodic structure created in such a manner P=Pi*D, where D is the diameter of the rope. Let Lp be the length of the tubes found within one period of the structure. As easy to find we have Lp/D=8.8858.

TWISTED PAIR - TYPE 2

The more clever way of twisting two ropes together is as follows:
(a) take two straight pieces of the rope and put them in parallel so that they do not touch - to make sure that it is the case insert a virtual cylinder of diameter d between them.
(b) start twisting symmetrically the pieces of the rope together so that they remain in touch with the virtual cylinder,
(c) do not stop twisting when the pitch reaches the Pi value,
(d) stop twisting, when the ropes come in touch with each other. (Do not forget to remove the virtual cylinder!)

In this conformation the radii of the spirals defining axial curves running inside the twisted ropes are slightly larger than the radii of the ropes: R1=R2=0.5229D. As a result, a small hole appears in the twisted pair structure along its long axis. The pitch of the structure is smaller than Pi: P=2.6967 D. The tubes touch each other along two spiral curves running between the tubes. The length of the rope per period Lp/D=8.5013.

TWISTED PAIR - TYPE 3

Take the most tight conformation of type 1, and (remaining all time at the limit above which overlaps between the tubes appear) start increasing the radius of the spiral formed by one of the ropes decreasing at the same time the radius of the spiral formed by the other one. Stop the process, when the first spiral becomes close packed. See below.

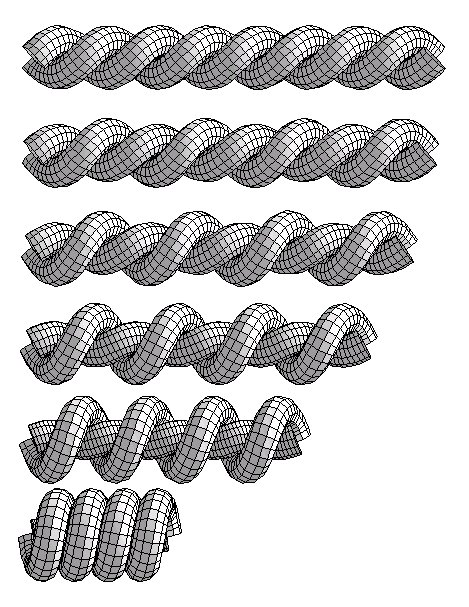
In this conformation the radii of the spirals defining axial curves running inside the twisted ropes are different, but their sum is equal D : R1=0.97326 D, R2=0.0267 D. Pitch of the structure is much smaller than previously: P=1.0136 D. The rope length per period Lp/D=7.2261. Note, that the value of R2 is limited by condition that the curvature of the inner spiral cannot be larger than 2/D.

TWISTED PAIR - TYPE 4

In the fourth and it seems best, conformation (we do not show its construction details because visually it differs too little from the third one) R1=0.9670D, R2=0.0377 D , thus, their sum is larger than 1. The minimal pitch P=1.0139D. The length per period Lp/D=7.2013.

Looking at the numbers cited above, one can immediately see the reasons for which during the tightening process the m-fold symmetry of the initial conformations of the T 2,m knots must be broken.

[1] S. Przybyl and P. Pieranski, In search of ideal knots III. Application of Maple V.4 to the problem of two ropes tightly twisted together, Pro Dialog, 6 , 18 (1998) (In Polish)

Back to the index page

Smooth rope wound tigthly on a corrugated rod