Knots do not necessarily live in the continuous 3D space.
All of them can be implanted into a 3D lattice, e.g. the cubic one.
When transferred into the lattice they loose a lot of freedom and their life becomes simpler.
Simpler does not mean easy or happy.
For instance the lattice knots may be asked to limit the space they occupy to the absolute minimum.
This is what Alexander Grosberg and his co-workers do to the poor beasts.
They limited the available space to a cubic-shaped piece of the cubic lattice and asked the knots to fill it perfectly.
Filling perfectly? It's not easy!!! Is it possible at all?
Well, when the size of the room is m×m×m, where m is even, it should be possible. The chance exists.
Having a chance, does not mean knowing how to take it. The task is by no means trivial.
Co-workers of Grosberg - Lua, Moore and Borovinskiy, know.
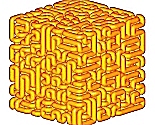
They managed to produce monster knots that fill perfectly a huge 14×14×14 cubic room.
Below you will find one of them.
Reminds a plumber's nightmare, doesn't it?
(The chief plumber sits in the shadow. Exhausted but happy. No wonder.)
I got the coordinates of the monster knot from Rhonald Lua. (Thanks!)
Imagine the tube is of human size so that you may enter it.
The entrance is in the lower left corner. The exit - to its right.
Walking along the tube you will visit each of the lattice sites located within the cubic room.
And you will visit each one time. The path is Hamiltonian.
But... of what type is the knot?
It's better to know, before entering the maze, don't you think?
Well, SONO managed to find it out.
Click
to learn, how it performes
the task. (In the example the knot is different.)If you want to learn the science of the monster knots, visit the home pages of Grosberg. Do it!