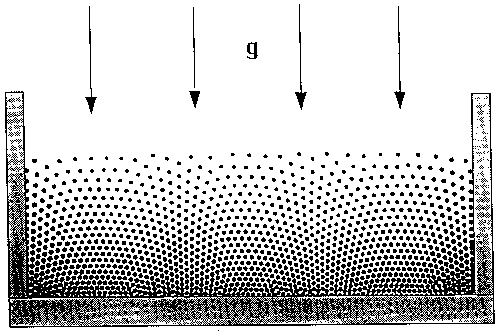
Gravity's rainbow : the hint provided by nature itself.
Consider a system of n
particles
in a 2-dimensional box, repulsing each other with long range forces. No
doubt, the ground state structure of such a system is very close to a
perfect
triangular lattice. Submerge the system within a strong, uniform
gravitational
field.
Which is the structure of its ground state now?
The question is by no means
trivial. One may expect that locally the hexagonal symmetry of the
triangular
lattice should be preserved. Thus, the ground state structure should be
built from hexagonal clusters - large at the top of the box, small,
compressed
by the gravitational field, at the bottom of the field. But, how to
built a sensible wall from bricks the dimension of which changes
continuously
with the height? The clever way to perform the task was indicated
by
the nature itself. Below you will find a picture taken in a laboratory
experiment with a set of magnetized (and thus repulsing) steel spheres
[1].

Gravity's rainbow : the hint provided by nature itself.
As seen in the figure, the local symmetry of the gravity's rainbow structure, as I have called it, is everywhere hexagonal. The nearest neighbor hexagons are small at the bottom and large at the top of the sample. What is it, what we see? How to describe it? The answer, suggested independently by K.W. Wojciechowski and F. Rothen, is: the ground state structure is very close to a conformally transformed triangular lattice [2-8]. The complex transformation applied by the nature in this case seems to be ln z. Figure below presents this case.

Nearly conformal structures were observed also in other experiments. Below, I present a picture taken by Florence Elias in her experiments on the ferrofluid froth.
Conformally transformed lattice of soap bubbles (numerical, of course), and its experimental, magnetic froth realization.
References
[1] P.Pieranski, Gravity's rainbow. Structure of a 2D crystal grown in a strong gravitational field, Proceedings of the NATO Advanced Study Institute, Geilo, 1989.
[2] F. Rothen, P. Pieranski, N. Rivier and A. Joyet, Cristaux conformes, Eur. J. Phys. 14, 227 (1993)
[3] N. Rivier, P. Pieranski and F. Rothen, Conformal crystals and their defects, Proceedings of the conference ‘Aperiodic 94’, Les Diablerets, 17-21, September 1994.
[4] F. Rothen, P. Pieranski, Mechanical equilibrium of conformal crystals, Phys. Rev., E 53, 2828 (1996)
[5] A. C. Branka, P. Pieranski, K. W. Wojciechowski, Confined planar mesoscopic suspensions in external field: Brownian Dynamics simulation, Chem. Phys., 204, 51 (1996).
[6] K. W. Wojciechowski, J. Klos and A. C. Branka, Do Conformal crystals Exist in Uniform Fields, in "Monte Carlo and Molecular Dynamics in Condensed Matter", Conference Proceedings, Vol. 49, Eds. K. Binder and G. Ciccotti, SIF, Bologna, (1996).
[7] K. W. Wojciechowski and J. Klos, Soft Condensed Matter in Strong Uniform Fields; Gravity's Rainbow Revisited, Journal of Physics A: Math. & General 29, 483 (1996).
[8] K. W. Wojciechowski, The inverse problem for conformal crystals in two- and higher-dimensions, in "Slow Dynamics in Complex Systems", Conference Proceedings, Eds. M. Tokuyama and I. Oppenheim, AIP 1999 (in print).
The name - gravity's rainbow -
flushed through my mind as for the first time I have seen the
conformal
beauty.
It flashed through it, because a week or two
before I lost a battle to read in original the Pynchon's
novel.
Polish translation has just been published
(2001).
A new battle is in front of me.